Making Physics fun tolerable
Chris is a Stanford-educated tutor with over 10 years experience tutoring Physics to students of all abilities, from students struggling to get from a C to a B, to go-getters trying to move an A- up to an A, to struggling students just hoping to pass. In that time he got a lot of experience learning how to explain this stuff in a way it actually makes sense to non-math people. Through his videos he has helped countless students, and he can do the same for you.
Physics
Units, Sig Figs & General Science Stuff
This chapter covers the basics of scientific notation, both converting it to regular numbers and back again. Decimals, huge numbers, multiplying scientific notation numbers together, positive exponents, negative exponents, "base 10", etc. it's all covered.
Sig figs. This chapter will teach them to you, but it's your job to remember to use them in every answer for the rest of the year or you'll lose half your points. Seriously.
The process of converting units, often called Dimensional Analysis, is one of the most important skills in science, and like sig figs you'll need it for the rest of the year.
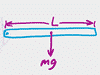
This chapter covers the general concepts of density and buoyancy, as well as how to calculate density and flotation forces on submerged and floating objects.
Converting between degrees Fahrenheit, Celsius, and Kelvin. Also covered: absolute zero, and why you always want to use Kelvin for gas problems.
This chapter introduces standard deviation, tells you what the heck it is and how to calculate it, and relates it to the normal distribution.
Not a long chapter, but one which explains something that's probably on your next lab report.
Vectors
Basics of vector addition, subtraction, multiplication, dot product, scalar product, magnitude, unit vectors, cross multiplication, and components.
This chapter covers how to do everything you need to do with vectors in physics, but especially the stuff you do constantly: breaking force and velocity vectors into their X & Y components, combining vector components back into a "resultant vector", and combining multiple vectors into one (like to find the net force vector) by breaking each into its components.
Motion
Reference frames are your easiest way to do better in physics (and get some partial credit along the way), so this video introduces what they are and shows you how to draw them in for several types of common kinematics problems.
This chapter shows you how to do the most common relative motion problems: moving walkways, boats rowing across current in a river, and planes.
DO NOT skip this chapter unless you are the A+ student in your physics class (every class has one). You'll find lots of videos on how to do "one dimensional" motion problems (either things going straight up and down or straight sideways), and there are also lots of "equation free" videos to help you get used to the concepts, to get you used to the units of acceleration that seem to trip everyone up, to introduce the formulas, and to show you how to work easier problems in your head so that you're less likely to get lost plugging and chugging. The more advanced videos in this chapter get into the formulas also shows you how to do the most common vertical and horizontal kinematics problems: objects dropped off buildings; objects thrown vertically up or down off a building; cars and buses accelerating down the road.
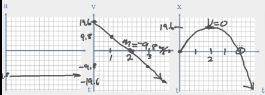
These videos cover graphs of acceleration, velocity and position in a similar way to how your calculus professor made you sketch the derivative of a function. The key takeaways are that you can use the slope of a curve to sketch its derivative, or you can use the "area under the curve" to plot its integral.
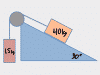
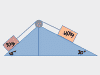
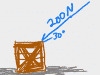
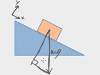
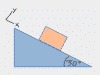
This chapter covers kinematic ramp problems WITHOUT friction or forces, and most importantly, it explains how to draw those dang triangles for ramp problems, where you have to break g into its X and Y components. Problem types covered are kinematic setups like: A skier heads down a 20° slope, how fast is she going after 30m; or, A box slides down a 15° ramp, how long does it take to reach the bottom? If you're using F=ma to solve all kinds of free body diagram situations on ramps, then look for the ramps videos further down.
Your class might not cover this, so make sure you have to know this before watching these videos, because this is an annoying topic. Basically it's 2-D kinematics, kind of like you would find in the projectiles chapter, except EVERYTHING is a vector with i's and j's in it, and EVERYTHING is pointlessly confusing! It's like your prof and book went out of their way to make 2-D motion as obscure and abstract as possible. Makes you wonder if they're out to get you. (Before this chapter, I would have said they aren't, but after this chapter, I'm not sure...)
This chapter covers every type of projectile motion problem that your physics prof (or pre-calc prof, for that matter) could throw at you. We'll start things off with the Range Equation, which can only be used for flat-field problems where the projectile lands at the same level it was launched from. Then we'll get into the various types of problems that have different levels, from projectiles shot upwards at castles to arrows shot down from castles onto fields below. And we'll wrap up with several videos on very specific types of harder problems you're likely to see, such as projectiles dropped from airplanes, calculating max height of a projectile, and that one where an arrow is launched at an object falling through the air.
These videos cover the most basic circular motion problems, the ones you get BEFORE your class does forces, Newton's Laws (F=ma), etc. In these videos we're just covering basic centripetal (and centrifugal) acceleration problems, including situations like satellites orbiting a planet, or a roller coaster going over the top of a hill. A later chapter of videos in the Forces section will cover advanced circular motion and F=ma problems.
Forces (F=ma)
This chapter covers all of the basic vocab and concepts that you could need for multiple choice and short answer questions about forces. Lots of vocab and intro to forces you should know: Tension, Springs (Hooke's Law), Weight (gravity), Normal Force, and Friction. Also covered are the difference between mass and weight, and contact and field forces.
This chapter covers those magical three Newton's Laws: Newton's First Law, Newton's Second Law, and Newton's Third Law. He was very creative with the names, that Newton guy.
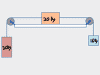
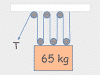
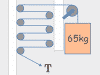
This chapter covers everything you could need to know about free body diagrams, starting with why the heck the darned things are called free body diagrams to begin with. Then each video shows you how to do the free body diagram for a common type of problem, from sliding boxes to inclined ramps and pulley systems.
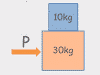
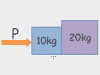
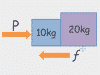
This chapter covers the word problems that the Forces chapter in physics class usually starts with. Given acceleration and mass, you may be asked to solve for net force, or given a bunch of different forces, you might need to find the net force (by combining the vectors into a single vector using vector components). Also covered are a favorite physics problem type: calculate the weight of something on the moon.
This chapter covers detailed examples of various problems that involve objects hanging from one or two ropes:
The videos in this chapter cover word problems about elevators, specifically the ones where they tell you how fast the elevator is accelerating up or down and then ask you how much the scale under the passenger would say the person weighs. Examples covered:
First, this chapter explains what the friction force is, how to calculate it, and how to use it in F=ma problems. Then it gets into a bunch of problems covering static friction. Examples covered:
.png)
This chapter covers detailed examples of problems involving an object, crate, or dog sled getting pushed or pulled across a level floor with or without friction:
.png)
.png)
.png)
This chapter covers detailed examples of ramp problems involving forces, where you have to: 1) create the free body diagram and not leave out anything; 2) work out your F=ma equations in X and Y; and 3) solve the equations using substitution. Examples covered:
.png)
.png)
The videos in this chapter cover one of the most difficult and time-consuming type of physics force problems that you'll come across: a force pushes or pulls two or three objects that are contacting each other, and you're supposed to find the force between them. Examples covered:
.png)
.png)
Atwood machines are a type of F=ma problem where there are at least two masses and a bunch of rope and pulleys, also known as a pulley system. Examples covered:
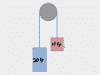
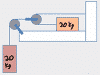
The videos in this chapter cover problems where a mass on a string is being swung around in a circle. Could be a yo-yo, getting whipped in a vertical circle or a horizontal circle around someone's head. Could be a mass on a frictionless table with a weight on the string in a hole in the middle of the table. In each problem, you'll be asked to calculate either the velocity or radius of the circle which would: cause the string to go slack, break the string, or achieve equilibrium. Examples covered:
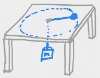
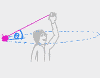
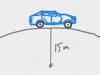
These videos cover lots of examples of centripetal force problems where the object going in a circle is a vehicle. In the case of roller coasters and jets (and some car problems), the circle is usually vertical and you're being asked to find the speed at which the person in the vehicle is "weightless" at the top of the loop (i.e. normal force is zero). In other car problems, the circle is horizontal (a curve in the road), and you're being asked how high to bank the turn or what coefficient of friction would prevent the car from sliding off the road. Examples covered:
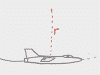
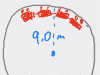
Work, Energy & Momentum
Work is sort of like effort: the harder you push, and the further you push for, the more energy you've put in. This being physics, sometimes a simple principle can look really complicated once it's in a word problem, so this chapter explains the concept and then covers tons of examples, from lifting things to pushing things to using kinetic energy to calculate the work a foot does on a soccer ball:
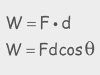
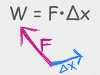
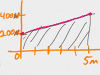
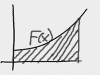
In many physics classes, power is one or two problems. In others, they make it more complicated. These videos cover Power in enough depth that you can handle the tough stuff, but it also makes it easy for you to skim and get what you need. And for those of you aspiring to be architects, designers, or restaurant entrepreneurs, as a bonus you also get a video about why Edison bulbs are your worst nightmare from a power and efficiency standpoint.
This chapter has ten videos covering every nook and cranny of Conservation of Energy. Personal favorites are Tarzan problems (pendulum problems in disguise) where the legendary jungle master swings up, down and sideways. Roller coasters are a teacher fave, because the roller coaster is going the same speed at all the places on the track that are at a given height, so you can do cool stuff like throw an unexpected centripetal force or work-energy theorem problem on the end. And of course we cover the basics like kinetic energy, spring potential energy, gravitational potential energy, conservative vs non-conservative forces, and runaway truck ramps.
This chapter covers all the different types of momentum and collision problems you're likely to see: 1-dimensional, 2-dimensional, elastic, inelastic, billiard balls, figure skaters, cannons, etc.
The videos in this chapter cover all the typical impulse problems you see: golf balls, baseballs, cars, etc. Mostly, though, I spend a lot of time explaining what you REALLY need to know about impulse: how the heck to tell when to use impulse (and momentum) vs when to use work (and energy)!
Rotational Motion
This chapter covers all the different types of momentum and collision problems you're likely to see: 1-dimensional, 2-dimensional, elastic, inelastic, billiard balls, figure skaters, cannons, etc.
This chapter starts with a video full of examples about how to use the rotational kinematics formulas to solve for angular acceleration, angular velocity, and angular displacement (Θ). The second video is about gear ratios, calculating the angular acceleration and velocity of on gear when you are given information about the other gear (or bike sprocket) that it's driving.
This topic covers what to do when linear quantities like velocity (m/s) are in the same problem as angular quantities (ω, radians, rad/sec, etc). This happens all the time in problems about cars and bikes, where they'll give you the distance driven or how fast the car is going and then ask you to figure out how fast the wheels are spinning. Also a cool problem: giving you the length (linear) of a string wrapped around a shaft (angular motion).
These videos cover what the moment of inertia is, what it means, and how to calculate it. Also covered is the Parallel Axis Theorem, which allows you to calculate the moment of inertia of an object when rotated around an axis other than its center of mass.
In addition to explaining what torque means and how to calculate it, in these videos we also endeavor to explore torque through the existential lens of the 1980's classic "Over The Top", a film exploring professional arm wrestling and truck driving (yes, arm wrestling) through a family story involving a young boy and his estranged father. This masterpiece stars Sylvester Stallone, whom many of you young punks won't know is the star of Rocky, another movie you may not know.
In this chapter we learn how to deal with torques when there are more than one torque acting on a single object. Much like we did with net forces, first you have to add and subtract the various torques to combine them into a single net torque before you apply Kinematics to them.
These videos cover difficult rotating body problems where you've got a rotating mass, like a heavy wheel or a kid's gyro toy, that gets rotated or "spun up" by a linear force like a rope or gravity. Examples covered:
As we previously discovered in linear motion, energy and work make most kinematic problems waaaaaaaay easier to solve than they would be with torque (τ), time, angular acceleration (α), angular displacement (Θ), etc:
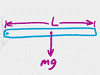
Rolling is more complicated than you'd think! On the one hand, you've got a mass on the move, so all the usual linear kinematics and energy formulas work. On the other hand, anything that is rolling is also rotating, which means it's got rotational kinetic energy too. It gets a bit complicated, but it's kind of cool if you study it because our lives are full of wheels:
Angular momentum is a lot like "regular" momentum: it's conserved. And bizarrely, even an object moving in a straight line has angular momentum. Crazy!